Stand volume
ANU

 Stand volume
Forest Measurement and Modelling.


Like tree bole volume, an estimate of the total bole volume in a stand or plot is important for forests quantification and management. Stand volume at a nominated age is related to the site quality, and the total at any time is important for an estimate of wood and biomass resource. Also like tree volume, stand volume is a function of stand height, average tree taper, average bark thickness and average diameter or basal area.

There are a number of practical approaches to the determination of stand volume:
  • Ocular estimate: An estimate of stand volume made by a skilled worker.
  • Sample tree: Select and measure the volume of an average tree, then inflate this value for the stand volume.
  • Enumerate the stand for dbh (and height) and use a tree volume table or equation to estimate the volume of each tree. Add the individual volume estimates to derive stand volume.
  • Derive and use a stand volume equation.


Ocular estimate In the beginning of the 19th Century, foresters in central Europe ocularly estimated the volume and stocking of small forest areas (called Forstorte). This approach to estimating stand volume provided adequate information for planning in the State Forests of Saxony until the early 1940's (Loetsch and Haller, 1964, p. 7). The main requirement for collecting effective volume information was the existence of a body of workers with sufficient experience and knowledge to estimate reliably the timber resources on small areas, and sufficient time to visit all the Forstorte. Workers skilled in ocular estimation were in great demand.

Brack (1996) demonstrates that skilled workers can still estimate stand volume to an acceptable level of precision. The reliability of ocular estimates can be determined by correlating ocular estimates of stand volume with measured volume. In the study reported by Brack (1996), local field foremen and foresters were able to predict the volume for Cypress Pine stands in western NSW to within 5 m^3/ha. The linear correlation between ocular estimate and measured stand volume was found to pass through the origin, with a slope not significantly different to 1. However correlations were much poorer when the same approach was attempted in the more heterogeneous forests of coastal NSW.
Sample tree The ideal example of this method involves the selection of one tree whose volume is equal to the mean tree volume for the stand. The volume of the selected tree is then determined and the stand volume estimated by inflating the sample tree volume by the number of trees in the stand.
V = v * N
where V denotes stand volume, v denotes sample tree volume, and N denotes number of trees in the stand.

Such an approach may be possible in small stands of relatively homogeneous trees, but there are a number of problems:
  • A tree of mean volume may not exist. All trees may be smaller and larger trees than average, i.e. above or below the mean volume. To overcome this problem, two or three may be sampled and the mean volume determined from this small sample. However, a statistically reliable sample may need a large number of trees. The ease and simplicity of the approach is lost as more trees are sampled. It is also difficult to assess the reliability of the volume estimate (precision or bias) if the mean volume tree is selected subjectively.

  • Finding the mean sized tree. Even if a tree of mean volume exists in a stand, it may be difficult to locate. The tree of mean volume may also have the mean basal area (quadratic mean dbh). Thus, enumerating the stand for dbh may allow the tree of mean basal area (or two to three trees around the mean) to be located and measured for volume.

    The tree that corresponded to mean basal area, mean height, mean taper and mean bark thickness might be expected to have a mean volume and so resources could be devoted to enumerating the stand for all these parameters. However, this would not be practical or worthwhile as the sum of the means does not necessarily equal the mean of the sums.

The accurate determination of the mean tree may not be as important if relative basal area instead of the number of trees is used as the inflation factor:

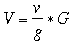where V denotes stand volume, v denotes sample tree volume, g denotes sample tree basal area and G denotes stand basal area.

Using basal area instead of stocking effectively turns the sample tree method into a stand tarrif or volume line where the intercept is assumed to be 0 and the slope of the line determined as v/g.

Tree volume equations / tables If one-way tree volume equations or tables exist, the stand can be enumerated for dbh and the tree volumes modelled and added together to get stand volume. If two-way equations are available, all trees in the stand can be measured for height in addition to dbh, or a stand height curve can be derived to predict height for a given dbh.

Some volume equations use a mixed of tree and stand parameters as independent variables. For example, tree bole volume (v) may be predicted using the tree basal area (g) and a measure of stand height (H) may be used instead of individual tree height:

Similarly, a ratio of merchantable volume (volume up to a merchantable diameter limit) to total volume has been correlated with tree and stand parameters. For example, Vanclay (1982) predicts the ratio (R) of merchantable volume to total volume using merchantable height for a tree (h) and mean predominant height (H). Merchantable volume is defined as the volume to a merchantable small end diameter or other limiting factor:

Where a volume line or tarrif based on tree basal exists, then stand volume can be determined without measuring individual tree basal area:

  • Estimate stand basal area (G in m^2/ha) using angle-count sampling or other simple technique.
  • Estimate trees/ha (N) by dividing G (above) by the basal area of the tree with quadratic mean diameter or other easy technique.
  • Calculate stand volume (m^3/ha) from the volume line:
    If tree volume v = a + b * g, then
    Stand volume V = (N * a) +( b * G)
    where a and b are constants and V, N, and G are per ha units.

Care must be taken to ensure that the equations or tables used are appropriate for the stand.
Stand volume equations Like tree volume equations, stand volume equations correlate stand volume to some expression of stand height (H), stand basal area (G) and stand form factor (F):
V = H * G * F

The stand form factor is not really the stand equivalent of the tree form factor, but is rather a more abstract value which incorporate the mean tree shape, the mean difference between average tree height and the stand height parameter used, and various interactions. However, stand volume estimation can be simplified considerably if F can be determined.

F can be determined empirically from stands that have been harvested:
F = V / (H * G)

This approach has been used for Pinus radiata plantations in NSW (where F is known as the k-factor). The estimates for the k-factor range up to 0.32 for mature stands (Brack, 1988). k-factors based on merchantable volume from thinning operations have also been empirically derived. These k-factors relate the basal area removed in a commercial thinning to the saleable volume. Merchantable k-factors can be as low as 0.15 for young plantations (about 15 years old), and grade up to 0.32 as the stand matures.

The stand volume equation can also be rearranged to give the following equality:
H * F = V / G
where the parameter H*F is termed the Form Height (Fh).

If Fh is known or can be easily predicted for a stand, then stand volume is easily determined by the multiplication of Fh with stand basal area (e.g. measured using an angle count sample). Form height has been linearly related to stand height (where V is total volume):

Alternatively, a volume equation similar to the Combined Variable, Australian or Form Factor equation could be derived. These stand volume equations would use stand basal area instead of tree diameter squared, and stand height instead of tree height.


Aerial volume equations / tables Parameters measured from aerial photographs can be used as independent variables stand volume equations. Estimates of stand height (mean or predominant - H), average crown width (w) and crown closure (C) can be determined from appropriately scaled aerial photographs. These values can be used to predict stand volume (V):

However, Avery and Meyer (1959) found that average crown width did not add significantly to the predictive power of the equation. Aerial volume tables based on the above equations were relatively common in northern America, but have not been extensively used in Australia.

Hamilton and Brack (1999) developed a series of equations that estimated stand volume from crown closure and median stand height measured from aerial photographs, and elevation (E) estimated from a Digital Elevation Model:

Species and crown form indices (an ordinal variable relating to the percentage of regrowth, regular and irregular crowns observed in aerial photographs) were added to the equation to predict merchantable volume.

Sample The mean volume of a sample of trees can be determined and then inflated to estimate stand volume. Where a high level of accuracy is not required, a subjective selection of the sample tree may be appropriate [as in the sample tree approach]. Where an unbiased estimate of stand volume is required, as well as a measure of the precision or reliability of the estimate, then an objective or statistically valid sampling frame is needed. Trees, selected randomly or systematically, could be measured for volume and then the mean volume inflated to estimate the stand volume.

As knowledge about the stand improves, more effective sampling approaches can be used. For example, without any knowledge of the population, simple random sampling would be appropriate. If the forester were aware of any structure in the population, e.g. fertility or altitudinal gradient, then a stratified sample would allow a better precision to be achieved. If however the forester knew there was no discernible pattern, a cluster sampling approach would achieve a similar precision for a substantially less cost. These types of sample selections are all equal probability based systems.

Variable probability sampling continues this use of forest knowledge to improve precision or reduce the cost of inventory. In variable probability sampling, sampling elements - in this case trees - are selected for measurement in proportion to some aspect of their value. For example, when the parameter of interest is volume, the most valuable trees will be the largest volume trees. A variable probability sample may therefore select trees in proportion to a simple auxiliary measurement like dbh or an assessor's ocular estimate of volume.

Variable probability sampling is also known as sampling with probability proportional to size (PPS) and is the basis of a wide range of schemes commonly mentioned in forestry literature: point- , line- , 3P / Poisson-, and list- sampling.

Pioneer work on variable probability sampling was begun during the Second World War. The theory and practical application of this work was developed during the following decade by Bitterlich (1947), Grosenbaugh (1952, 1955, 1958) and others. Australian forestry practice has been slow to take up the power of these developments and only angle count sampling is used in any routine sense in the major forest management organisations.

The basic principle in probability-based sampling is that the total population volume can be estimated from the volume of a sample divided by the probability of that sample being chosen: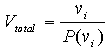

where vi denotes the measured volume of i and P(vi) denotes the probability of selecting i in the sample.

[s_volume.htm] Revision: 6/1999
Cris.Brack@anu.edu.au