Techniques for measuring height
ANU

 Techniques for measuring height of a standing tree
Forest Measurement and Modelling.


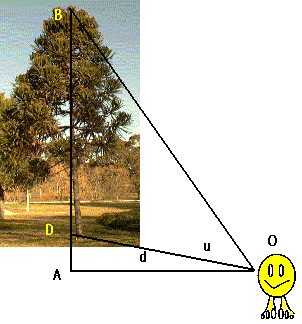
The height of a tree can be measured directly or indirectly. The direct measurement techniques can generally only be used on felled trees or small trees. Taller, standing trees are normally measured indirectly using an instrument commonly called a hypsometer.

Hypsometers are used to measure angles and distances to points on the tree from which height is derived. Geometric (similar triangles) or trigonometric (sin, cos and tan of angles) principles are embodied in the use of hypsometers. The correct use of a hypsometer will depend on the state of the tree (leaning or vertical) and the position where the observer can see the tree (observer's eye upslope or downslope with respect to the base of the tree).
Height stick (graduated pole) The use of height sticks is a reliable technique for measuring the height of trees less than about 25 m. Errors in measuring height are typically less than about 1%. Trees taller than 25 m take much longer to measure safely.

Height sticks are usually about 1.5 m long and constructed of tubular duralumin or fibreglass. A base stick is typically, l.5 m in length, and graduated in decimeters. Essentially, the poles are pushed up along the bole until the top of the stack of sticks is level with the tip of the tree.

See the Code of Forest mensuration Practice, section 2.1.2 at http://www.anu.edu.au/Forestry/mensuration/rwg2/code/2-1-2.htm for detailed instructions on use.
Climbing the tree Climb the tree to the maximum safe height. The distance from this height to the ground can be measured using a tape, while the distance from this safe point to the tip of the tree can be measured using a calibrated pole.

Safe climbing techniques should be used at all times.
Observer uphill from vertical tree
  1. Stand where you can see both the base and tip of the tree. Some hypsometers specify the [horizontal distance] OD (e.g. 15 or 20 m).
  2. Site down to the base of the tree and, depending on the hypsometer, record the angle d or the value AD.
  3. Site up to the tip of the tree and record the angle u or the value DB.
  4. Height = AD + DB or OD x (tan(u) + tan(d))
Observer downhill from vertical tree
  1. Stand where you can see both the base and tip of the tree. Some hypsometers specify the [horizontal distance] OA (e.g. 15 or 20 m).
  2. Site down to the base of the tree and, depending on the hypsometer, record the angle d or the value AD.
  3. Site up to the tip of the tree and record the angle u or the value AB.
  4. Height = AB - AD or OA x (tan(u) - tan(d))
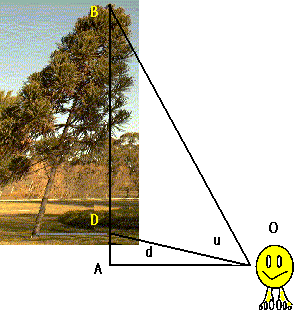
Observer uphill from leaning tree
  1. Stand where you can see both the base and tip of the tree. Some hypsometers specify the [horizontal distance] OD (e.g. 15 or 20 m).
  2. Find the point A that is directly beneath the tip. Note that the distance OD is the horizontal distance from the observer to a point directly beneath the tip - it is not to the base of the stem.
  3. Site down to point A and, depending on the hypsometer, record the angle d or the value AD.
  4. Site up to the tip of the tree and, record the angle u or the value DB.
  5. Height = AD + DB or OD x (tan(u) + tan(d))
Observer downhill from leaning tree
  1. Stand where you can see both the base and tip of the tree. Some hypsometers specify the [horizontal distance] OA (e.g. 15 or 20 m).
  2. Find the point D that is directly beneath the tip. Note that the distance OA is the horizontal distance from the observer to a point directly beneath the tip - it is not to the base of the stem.
  3. Site down to point D and, depending on the hypsometer, record the angle d or the value AD.
  4. Site up to the tip of the tree and, record the angle u or the value AB.
  5. Height = AB - AD or OA x (tan(u) - tan(d))

[height.htm] Revision: 6/1999
Cris.Brack@anu.edu.au