Stand Basal Area is a useful parameter for the forest mensurationist because it is relatively easily collected and can be related to many other parameters of interest (e.g. site density and stand volume). The internationally accepted symbol for stand basal area is G (m^2 ha^-1) and for tree basal area, g (m^2). G is an important reference variable for a stand and is particularly useful in quantitative description.

G values commonly range from 10 to 60 m^2 ha^-1 in both coniferous and hardwood forests. In rare cases, G values of 150 m^2 ha^-1 may be reached on exceptionally good sites.

G is the sum of the basal areas of all (living) trees, in the stand. G is derived by reference to tables or by summation by calculator:

G (square metres) = 0.000 078 539 8 x d^2, where d is DBH in cm.

Note: 0.000 078 539 8 is (PI/40 000). The division by 40 000 corrects for the difference in units (cm and m) and diameter to radius.

G is usually expressed over bark and on a unit area basis, e.g. m^2 / ha.

Stand mean BA is also a useful stand variable. It is calculated as G/N, where N is the number of trees in the stand. The diameter equivalent to g is called the QUADRATIC MEAN DBH:
dg = sqrt( (G / N) x 40000 / PI)
where dg is the international symbol for quadratic mean DBH.

The quadratic mean DBH is preferable to the arithmetic mean DBH as a size parameter of trees in a stand because of the additional weight it gives to the larger diameters.

Estimating stand basal area

The basal area of a forest stand is estimated by sampling in one of two ways:-

• fixed area plots
• variable radius plots. Also known as angle count or point sampling as well as other names.

Fixed area plots

The DBH of each tree is measured using circular, rectangular or square sample units (plots) and mean stand basal area (G) is determined by totalling the basal area of each tree in the plot, and dividing by the area of the plot. Sampling using fixed area plots is not as efficient as angle count sampling for estimating G.

Angle count sampling

When a population mean depends more on the size of large compared with small units, it is more efficient to select the larger units with greater probability. This technique is called PPS Sampling or sampling with Probability Proportional to Size.

This principle has been applied to various forest sampling problems but most notably to estimating basal area per unit area by angle counting, where inclusion of a tree in the count depends on the basal area of the tree and its proximity to the sampling point, ie small trees are not included if they are some distance from the sampling point, while larger trees will be included at even greater distances.

Angle count sampling estimates G per unit area of a stand without measuring:

• the g of any tree in the stand or
• the area of ground surface sampled.

The method was developed by an Austrian forester Dr W. Bitterlich in the late 1930s and perfected in the late 1940s. Its application was recognised by Cromer (1952) in Australia and Grosenbaugh (1952) in the USA ahead of European foresters. In the literature, it is referred to under various names, namely:

• Angle count sampling
• Point sampling
• PPS sampling
• Variable radius plot sampling (VRP sampling)
• Plotless cruising or plotless survey.

Angle count sampling procedure

• Select the angle count spot
• Count within a complete circular sweep the number of trees whose diameters at breast height subtend angles at the operator
• larger than a certain reference angle (n1)
• equal to a certain reference angle (n2).
• Add n1 and 0.5 x n2 and then multiply the result by a factor (BAF) appropriate to the reference angle.

Principle of angle count method

A simple "mind experiment" might help explain the principle of the method:

Imagine that there exists a forest with only small and large diameter trees (e.g. 10 cm and 50 cm DBH respectively) for which we want to determine stand basal area. A single 10 cm DBH tree only has a basal area of 0.00785 m^2 while each 50 cm tree is 0.196 m^2 (= PI * Radius^2 ). We do not want to waste time measuring too many small trees, but do not want to miss the big values contributed by the large trees, so we use 2 circular plots of 5 m and 25 m radius and measure only small and large trees respectively within each plot.

Now imagine that we established our plots and found that there were 3 small trees within the 5 m radius plot and 4 large trees within the 25 m radius plot. The stand basal area would be calculated as:

10 cm tree contribution:        
 = 3 * (PI * Radius(tree)^2 ) / (PI * Radius(plot)^2) (m^2/m^2)
 = 3 * (PI * 0.05^2) / (PI * 5^2) (m^2/m^2)
 = 3 * 0.00785 / 78.5 (m^2/m^2)
 = 3 * 0.00001 (m^2/m^2)
 = 3 * 0.00001 * 10000 (m^2/ha)
 = 3 * 1 (m^2/ha)


50 cm tree contribution:
 = 4 * (PI * 0.25^2) / (PI * 25^2)  (m^2/m^2)
 = 4 * 0.196 / 1960 (m^2/m^2)
 = 4 * 0.00001 (m^2/m^2)
 = 4 * 0.00001 * 10000 (m^2/ha)
 = 4 * 1 (m^2/ha)


Stand basal area        = 3 + 4 (m2/ha)  = 7 (m2/ha)

But of course a real forest would have trees of a range of DBH values. We could therefore establish a range of plots for all the different DBH classes. For example, our imaginary forest above might also have trees of 20, 30 and 40 cm DBH which we could sample in circular plots of 10, 15 and 20 m radius respectively. Using the same calculations as above therefore, we would find that each 20, 30 or 40 cm DBH tree that is within its 10, 15 or 20 m radius plot adds 1 m^2/ha to the overall stand basal area. Now that is the important part of the matter! We have set up our plot dimensions so that each tree of X cm DBH adds 1 m^2/ha to the stand basal area if it is within a radius X/2 m of the plot centre - where X is any number. In fact, we no longer even need to know what is the value of X. All we need to know is whether the ratio of DBH to distance from the plot centre is greater than 2 cm : 1 m. If the ratio of DBH : Distance is greater than 2 cm : 1 m (1 : 500), then the tree of whatever DBH is within its respective plot and that tree adds another 1 m^2/ha to the estimate of the total stand basal area. An optical wedge, Dendrometer II, Spiegal Relakop or similar instrument simply helps determine if the ratio of DBH : Distance away exceeds the critical ratio and therefore whether the tree is within the plot and adds to the estimate of stand basal area.

Note that a tree of X cm DBH is within its respective plot when the ratio of DBH : Distance from centre exceeds 2 * X cm : X m. Thus a tree of 20 cm DBH is counted if it is anywhere from 10 m away right up to the exact plot centre! A tree is either in or out of the plot - a 20 cm tree right at the centre is no more or less within the plot than a similar tree that is 3, 6 or 9 m away from the centre.

Alternatively, the following argument may help explain the pinciples:
Assume:

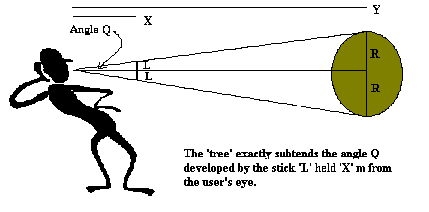
• the ground is level
• an observer is standing Y metres from a tree of radius R metres. He is holding X metres from his eye a horizontal stick 2L metres long which is at right angles to his line of sight to the tree. Thus, the angle Q depends on X and L.

Now:

• The area of acceptance for trees of radius R is
  = (PI x Y^2/10 000) ha
  (This is the area within which a tree of radius R will appear "bigger" than the 2L stick.)
• and the basal area of a tree of radius R is
  = (PI x R^2) m^2
• If then there are n trees are of size R, then the basal area of these trees is
  = n x PI x R^2 (m^2)
• The stand basal area (G) of these n trees is then
  = n x PI x R^2/(PI x Y^2/10 000) (m^2/ha)
  = n x 10 000 x R^2 / Y^2 (cancelling out PI)
• or alternatively by trigonometry, G
  = n x 10 000 x Sin^2Q
• If there are also m trees of radius S, the basal area (m^2/ha) = m x 10 000 Sin^2Q
• Thus, total G = N 10 000 Sin^2Q where N denotes all the trees with a radius that appears bigger than 2L.

The value 10 000 Sin^2Q, (which is the equivalent to 10 000 x R^2 / Y^2) is known as the basal area factor or BAF. Stand basal area = N x BAF.

Angle count instruments

Collectively, instruments used in angle count sampling procedures are termed angle gauges. Built into each gauge is a certain reference angle. When using an angle gauge, this reference angle is compared with the angle subtended at a fixed point (the angle count spot) by the sides of a tree (usually at breast height). If the subtended angle is larger than the reference angle, then the tree is included in the angle count.

Instruments include:

• Relaskop
• Wedge Prism
• Calibrated thumb or other angle generating device

Practical aspects when using angle count instruments

• When sweeping, use an assistant carrying a 'T' piece to define the DBH point. The cross bar of 'T' is a 1.3 m so that the correct height for measurement is easily seen. If the T piece is positioned behind the tree so that the arms of the T extend beyond either side of the bole, then is is easier to determine if the reference angle is exceeded.
  An experienced observer only needs the 'T' piece in the borderline situation.
• Trees can be missed in sweeping dense stands. This error can be avoided in plantation stands by proceeding by rows.
• When using a wedge prism, hold the wedge precisely over the angle count spot at all times. This point, and not the observer's eye, is where the reference angle is generated. In contrast, when using the Spiegel Relaskop, thumb, etc., the angle is generated at the observer's eye and so the user's eye must be precisely above the angle count spot.
• When using a wedge prism, hold the wedge in a vertical position at any convenient distance from the eye and at right angles to the line of sight. View through the centre of the wedge. These precautions are necessary to avoid error.
• The number of borderlines (i.e. trees not clearly greater or smaller than the reference angle), in general, should not exceed 10% of the total count. The only reliable way to avoid operator bias with borderline trees is to:
• measure tree DBHOB (d)
• calculate for the BAF of the angle count instrument, the maximum distance (LD) from the angle count point within which a tree of that d is counted.
• LD = d / (2 x sqrt(BAF)) (d in cm and D in m).
• compare this calculated limiting distance (LD) with the actual distance (D) from the centre of the tree to the sampling point:
• If D > LD, the tree is OUT (not counted)
• If D = LD, we have a true borderline (count as half)
• If D < LD, the tree is IN.
• NOTE: Checking borderline trees when sweeping with a Spiegel Relaskop requires measurement of slope angle as well as dbhob.
• One cannot overstress the need to check borderline trees by direct measurement. Angle-count sampling is often used in resource inventory where the intensity of sampling is much less than 0.1%, i.e. one tree in a sweep actually represents at least 1000 trees in the population. If that one tree is a doubtful/near borderline tree and it is worth $20 on the stump, then $20 000 hinges on the decision whether the tree is 'in' or 'out'. Should not such a decision be made with extreme care?
• Trees wrongly counted lead to an error in BA estimation equal to the BAF in m^2 / ha.
• Thus, one must compromise in selecting the BAF to use. A small factor instrument (low strength) will result in a count of many trees with a greater likelihood of a wrong count but a relatively small error from a wrong count. A large factor instrument (high strength) will result in a low count with less likelihood of a wrong count but a large error if a wrong count is made.
• Too many 'IN' trees in a sweep makes the assessment rather tedious whilst too few leads to relatively low precision. A satisfactory compromise is a count of 7-12 trees per sample point. In Australian forests, basal area per hectare of fully stocked stands frequently lies in the range 20-50 m^2 / ha suggesting BAF values of 2 to 5. For heavily thinned stands and young poorly stocked crops, basal areas of 10-20 m^2 / ha are common suggesting BAFs of 1 to 2.
• Check for slope and correct if necessary. Determine the maximum slope (Q) that goes through the angle sample point and correct the estimated stand basal area:
  G = N x BAF x Sec(Q)
  Note that the Speigal Relaskop corrects automatically for slope so this correction is not needed.

Establishing angle count spots

• If the basal area of a forest stand is required, select a number of points either systematically (point-sampling grid on a map) or by some random process. Use the same factor gauge at each point. Varying the BAF leads to problems in the statistical analysis of the data. (If the structure of the forest is heterogeneous, an acceptable procedure is to stratify the forest prior to assessment and select a gauge of appropriate strength for each stratum). In both cases it is important to exclude bias in marking the sample point in the field. Pacing the distance between successive sample points may be permissible provided one does not (consciously or unconsciously) veer away from the specified bearing or alter one's pace to prevent the sample point being, say, hard up against a rocky outcrop or inside a large clump of nettle. One way to prevent such personal bias is to pace out part of the distance only and measure the last 20 metres or so by tape, keeping to the exact bearing. Statistically speaking, each point within the stand qualifies as an independent sample point, i.e. two points only a metre apart could provide two independent estimates of basal area for a given stand even though the individual trees included in both samples may be the same or differ by only one or two trees. In practice, however, one will try to prevent such overlap. This means that the distance between plot centres will have to be more than double the marginal distance of the largest trees likely to be encountered in the stand.
• A rough guide to the number of sampling points required in reasonably uniform stand conditions is given below:-

Area (ha)	No. of Sampling Points
0.5 - 2.0	8
2.0 - 10.0	12
over 10.0	16

• Where the crop is more variable, the number of sample points should be increased. The number of points required will vary with the error limits specified and the size and variability of the forest stand. A rough estimate of the number required can be obtained from a pilot sample using the formula:
• N = (Ct/e)^2 ,
• where N denotes the estimated sample size,
• C denotes the coefficient of variation of the pilot sample in percent,
• t denotes Student's-t read from a table for the appropriate number of degress of freedom attached to the pilot sample and probability level (at the 95% level of confidence, this value is usually set at 2),
• e denotes the error limits (desired standard error of estimate) specified in percent.
• Accurate use of angle count instruments requires much practice. In particular, when using instruments with small BAFs, e.g. 0.5, there is a tendency to underestimate basal area.

Disadvantages of Angle Count Sampling

• The method estimates G from a sample so the estimate is subject to sampling error. The precision in a series of estimates will depend on:
• size of sampling unit, i.e. BAF of angle gauge
• variation of G in the area under study
• experience of operator.
• The stocking density (number of trees) per hectare or per size class is not given directly. This information can be derived by having the assistant measure the DBH of each tree counted in the sweep. Then:
• G ha^-1 of each d class = No. of trees in class x BAF
• and No. of trees ha-1 in class= G (of class)/g(equivalent. to mid-class d ).
• Usually, it is cheaper, and more reliable, to lay out temporary plots and count.
• Remember that in sampling for stocking as opposed to basal area, probability is no longer proportional to size but to frequency of occurrence. Bounded plots are more appropriate in this case.
• It is sometimes difficult to obtain a clear unimpeded view in unpruned stands or in stands with heavy undergrowth. Of 82 angle count plots established in native hardwood stands (dry to wet sclerophyll) in the Cotter catchment in 1973, vision was impeded in only about 10% of the plots. Using a higher BAF (Spiegel Relaskop) and moving on the radius overcame most of the sighting problems. G s ranged from 5 to 50 m^2ha^-1.

Some Experiences with Angle Count Sampling

Van Laar (S. Afr. J. For. 72: 1-6 (1970)) estimated G in 77 sample plots using the Spiegel Relaskop, a wedge prism and calipers. He found:

• Differences in the G estimates by wedge and caliper were insignificant;
• The Spiegel Relaskop underestimated G by 4% compared to the calipers - an insignificant difference;
• The tendency with the angle count instruments was to count too many border line trees (checking the borderlines would eliminate this error!).
• Angle count sampling reduced the cost of field work by 50%.

Whyte and Tennent (N.Z. J. For. 20 (1): 134-47, 1975) point out that whenever angle count and bounded plot estimates of mean basal area per unit of area are compared, foresters almost invariably assume that the bounded plot gives the correct value, and this is then used to judge the accuracy of the angle count estimate. This assertion is quite wrong since a theoretically unbiased estimate of mean basal area should sample in proportion to stem basal area, not stem frequency. Bounded plot sampling does not achieve this whereas angle count sampling does. Both samples, however, provide only estimates of the true population mean. Each is subject to sampling error.

Publications by Palley and O'Reagan (For. Sci. 7: 282-93, 1961) and Kulow (J. For. 64: 469-74, 1966) also attest to the superiority of angle counting in accuracy and precision for estimating mean stand basal area. However, all authors agree that bounded plots are more efficient for determining stocking density (number of stems per unit area).